二次剩余问题之前就遇到过,但未深入学习过,也未做过记录,今天来补充。
什么是二次剩余
指一个整数n,如果存在一个整数x,使得$x^2 \equiv n \pmod p$,那么n就是p的一个二次剩余。其中,p是一个正整数,x是一个整数。如果不存在这样的x,那么n就是p的一个二次非剩余。
判断方法
Euler判别法
当且仅当$a^{\frac{p-1}{2}} \equiv 1 \pmod p$,a是p的二次剩余,即方程有解
当且仅当$a^{\frac{p-1}{2}} \equiv -1 \pmod p$,a是p的二次非剩余,即方程无解
勒让德符号(Legendre)
引入勒让德符号:
$(\frac{a}{p}) = \left{ \begin{matrix} 1,a在模p意义下是二次剩余\-1,a在模p意义下是非二次剩余\0,a\equiv0 \pmod p \end{matrix} \right.$
有结论:
$(\frac{a}{p}) \equiv a^{\frac{p-1}{2}} \pmod p$
如何解二次同余方程
前提,p为奇素数(不能被2整除的素数,是素数中的特例)。
定理一
对于上述同余方程,共有$\frac{p-1}{2}+1$个n的值能使方程有解,$+1$为n=0的情况。
定理二
设a满足$\omega = a^2-n$是模p的非二次剩余,那么:
$x\equiv (a+\sqrt \omega)^{\frac{p+1}{2}}$是二次同余方程$x^2 \equiv n \pmod p$的解。
相关算法
特殊情况
对于同余方程$x^2 \equiv n \pmod p$,且有$p \mod 4 \equiv 3$
那么$n^{\frac{p+1}{4}} \mod p$为一个解
Atkin算法
满足$p \mod 8 \equiv 5$,令$b \equiv (2n)^{\frac{p-5}{8}}\pmod p$和$i \equiv 2nb^2 \pmod p$
此时$i^2 \equiv -1 \pmod p$且$nb(i-1) \pmod p$为一个解。
Tonelli–Shanks 算法

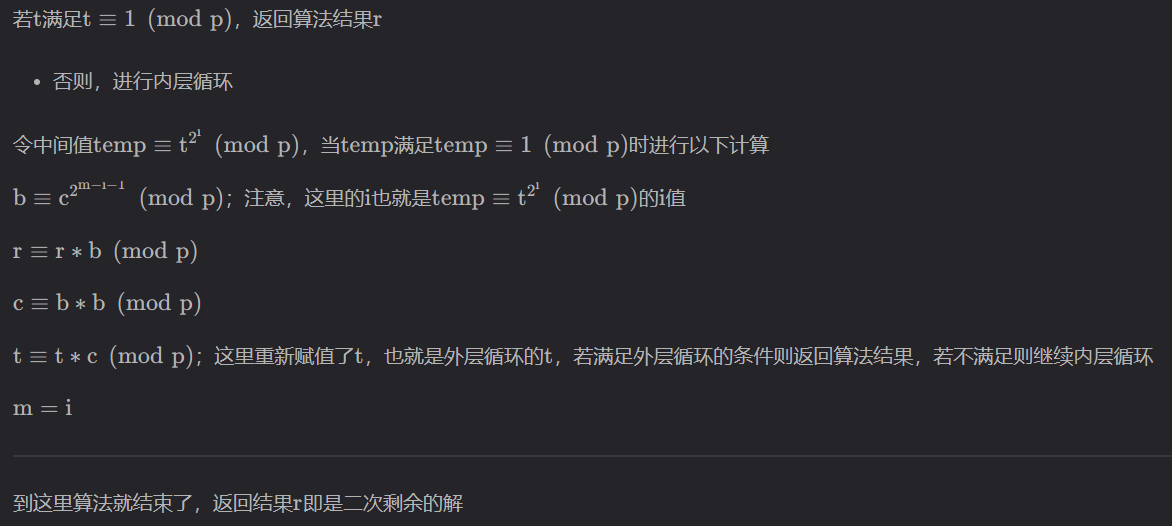
代码实现:
def Legendre(n,p): #这里用勒让德符号来表示判断二次(非)剩余的过程
return pow(n,(p - 1) // 2,p)
def Tonelli_Shanks(n,p):
assert Legendre(n,p) == 1
if p % 4 == 3:
return pow(n,(p + 1) // 4,p)
q = p - 1
s = 0
while q % 2 == 0:
q = q // 2
s += 1
for z in range(2,p):
if Legendre(z,p) == p - 1:
c = pow(z,q,p)
break
r = pow(n,(q + 1) // 2,p)
t = pow(n,q,p)
m = s
if t % p == 1:
return r
else:
i = 0
while t % p != 1: #外层循环的判断条件
temp = pow(t,2**(i+1),p) #这里写作i+1是为了确保之后内层循环用到i值是与这里的i+1的值是相等的
i += 1
if temp % p == 1: # 内层循环的判断条件
b = pow(c,2**(m - i - 1),p)
r = r * b % p
c = b * b % p
t = t * c % p
m = i
i = 0 # 注意每次内层循环结束后i值要更新为0
return r
sympy库中的nthroot_mod()函数也可用与求解同余式$n^{index} \equiv x \pmod p$
from sympy.ntheory.residue_ntheory import nthroot_mod
x=nthroot_mod(n,index,p)
我只是知识的搬运工,相关证明可参考:
Tonelli-Shanks算法_python_M3ng@L的博客-CSDN博客
相关例题
[V&N2020 公开赛]easy_RSA
from random import randint
from gmpy2 import *
from Crypto.Util.number import *
def getprime(bits):
while 1:
n = 1
while n.bit_length() < bits:
n *= next_prime(randint(1,1000))
if isPrime(n - 1):
return n - 1
m = bytes_to_long(b'flag{************************************}')
p = getprime(505)
q = getPrime(512)
r = getPrime(512)
assert m < q
n = p * q * r
e = 0x10001
d = invert(q ** 2, p ** 2)
c = pow(m, 2, r)
cipher = pow(c, e, n)
print(n)
print(d)
print(cipher)
'''
7941371739956577280160664419383740967516918938781306610817149744988379280561359039016508679365806108722198157199058807892703837558280678711420411242914059658055366348123106473335186505617418956630780649894945233345985279471106888635177256011468979083320605103256178446993230320443790240285158260236926519042413378204298514714890725325831769281505530787739922007367026883959544239568886349070557272869042275528961483412544495589811933856131557221673534170105409
7515987842794170949444517202158067021118454558360145030399453487603693522695746732547224100845570119375977629070702308991221388721952258969752305904378724402002545947182529859604584400048983091861594720299791743887521228492714135449584003054386457751933095902983841246048952155097668245322664318518861440
1618155233923718966393124032999431934705026408748451436388483012584983753140040289666712916510617403356206112730613485227084128314043665913357106301736817062412927135716281544348612150328867226515184078966397180771624148797528036548243343316501503364783092550480439749404301122277056732857399413805293899249313045684662146333448668209567898831091274930053147799756622844119463942087160062353526056879436998061803187343431081504474584816590199768034450005448200
'''
已知关系
- $d\cdot q^2 \equiv 1 \pmod {p^2}$
- $m^2 \equiv c \pmod r$
- $cipher \equiv c^e \pmod n$
- $n = p\cdot q \cdot r$
其中$n、d、cipher$已知,且$m < q$
通过getprime函数可知,生成的素数为光滑数。直接分解n得到p、q、r。然后常规RSA解出c。最后便是二次剩余问题了,用下算法即可:
n = ...
d = ...
cipher = ...
e = 0x10001
p = 102634610559478918970860957918259981057327949366949344137104804864768237961662136189827166317524151288799657758536256924609797810164397005081733039415393
q = 7534810196420932552168708937019691994681052660068275906973480617604535381306041583841106383688654426129050931519275383386503174076258645141589911492908993
r = 10269028767754306217563721664976261924407940883784193817786660413744866184645984238866463711873380072803747092361041245422348883639933712733051005791543841
phi = (p-1)*(q-1)*(r-1)
d = inverse(e,phi)
c = pow(cipher,d,n)
def Legendre(n,p): #这里用勒让德符号来表示判断二次(非)剩余的过程
return pow(n,(p - 1) // 2,p)
def Tonelli_Shanks(n,p):
assert Legendre(n,p) == 1
if p % 4 == 3:
return pow(n,(p + 1) // 4,p)
q = p - 1
s = 0
while q % 2 == 0:
q = q // 2
s += 1
for z in range(2,p):
if Legendre(z,p) == p - 1:
c = pow(z,q,p)
break
r = pow(n,(q + 1) // 2,p)
t = pow(n,q,p)
m = s
if t % p == 1:
return r
else:
i = 0
while t % p != 1: #外层循环的判断条件
temp = pow(t,2**(i+1),p) #这里写作i+1是为了确保之后内层循环用到i值是与这里的i+1的值是相等的
i += 1
if temp % p == 1: # 内层循环的判断条件
b = pow(c,2**(m - i - 1),p)
r = r * b % p
c = b * b % p
t = t * c % p
m = i
i = 0 # 注意每次内层循环结束后i值要更新为0
return r
m = Tonelli_Shanks(c,r)
print(long_to_bytes(m))
D^3CTF d3qcg
from Crypto.Util.number import *
import random
from random import randint
from gmpy2 import *
from secret import flag
import hashlib
assert b'd3ctf' in flag
Bits = 512
UnKnownBits = 146
class QCG():
def __init__(self,bit_length):
p = getPrime(bit_length)
a = randint(0,p)
c = randint(0,p)
self._key = {'a':a,'c':c,'p':p}
self.secret = randint(0,p)
self.high = []
def Qnext(self,num):
return ((self._key['a'])*num**2+self._key['c'])%self._key['p']
def hint(self):
num = self.secret
for i in range(2):
num = self.Qnext (num)
self.high.append(num>>UnKnownBits)
def get_key(self):
return self._key
def get_hint(self):
return self.high
Q1 = QCG(Bits)
print(Q1.get_key())
#{'a': 3591518680290719943596137190796366296374484536382380061852237064647969442581391967815457547858969187198898670115651116598727939742165753798804458359397101, 'c': 6996824752943994631802515921125382520044917095172009220000813718617441355767447428067985103926211738826304567400243131010272198095205381950589038817395833, 'p': 7386537185240346459857715381835501419533088465984777861268951891482072249822526223542514664598394978163933836402581547418821954407062640385756448408431347}
Q1.hint()
print(Q1.get_hint())
#[67523583999102391286646648674827012089888650576715333147417362919706349137337570430286202361838682309142789833, 70007105679729967877791601360700732661124470473944792680253826569739619391572400148455527621676313801799318422]
enc = bytes_to_long(hashlib.sha512(b'%d'%(secret)).digest())^bytes_to_long(flag)
print(enc)
# 6176615302812247165125832378994890837952704874849571780971393318502417187945089718911116370840334873574762045429920150244413817389304969294624001945527125
想求flag就必须先求secret,对于secret,有下面的关系:
$num_1 = a \cdot secret^2 + c \pmod p$
$num_2 = a \cdot num_1^2 + c \pmod p$
$high[0] = num_1 >> 146,high[1] = num_2 >> 146$
$a、c、p、high[0]、high[1]$已知。
显然得想办法恢复出完整的$num_1$来。
对于$num_i$,高位记作$h_i$,低位记作$l_i$,那么$num_2 = a \cdot num_1^2 + c \pmod p$可写成:
$h_2+l_2 = a \cdot (h_1+l_1)^2 + c \pmod p$
$a \cdot (h_1+l_1)^2 - (h_2+l_2) + c \equiv 0 \pmod p$
高位$h_i$我们是知道的,大概365位。低位$l_i$不知道,有146位。
显然需要构造二元copper解。
a = ...
c = ...
p = ...
hint = [..., ...]
enc = ...
def small_roots(f, bounds, m=1, d=None):
if not d:
d = f.degree()
R = f.base_ring()
N = R.cardinality()
f /= f.coefficients().pop(0)
f = f.change_ring(ZZ)
G = Sequence([], f.parent())
for i in range(m + 1):
base = N ^ (m - i) * f ^ i
for shifts in itertools.product(range(d), repeat=f.nvariables()):
g = base * prod(map(power, f.variables(), shifts))
G.append(g)
B, monomials = G.coefficient_matrix()
monomials = vector(monomials)
factors = [monomial(*bounds) for monomial in monomials]
for i, factor in enumerate(factors):
B.rescale_col(i, factor)
B = B.dense_matrix().LLL()
B = B.change_ring(QQ)
for i, factor in enumerate(factors):
B.rescale_col(i, 1 / factor)
H = Sequence([], f.parent().change_ring(QQ))
for h in filter(None, B * monomials):
H.append(h)
I = H.ideal()
if I.dimension() == -1:
H.pop()
elif I.dimension() == 0:
roots = []
for root in I.variety(ring=ZZ):
root = tuple(R(root[var]) for var in f.variables())
roots.append(root)
return roots
return []
h1 = hint[0] << 146
h2 = hint[1] << 146
P.<l1,l2> = PolynomialRing(Zmod(p))
f = a*(h1 + l1)^2 + c - (h2 + l2)
l1,l2 = small_roots(f,[2^146,2^146],m=4,d=4)[0]
num1 = h1 + l1
print(num1)
m和d的取值有待考究。
defund/coppersmith: Coppersmith’s method for multivariate polynomials (github.com)
求出$num_1$后,看第一个式子:
$num_1 = a \cdot secret^2 + c \pmod p$
$secret^2 = a^{-1}\cdot (num_1 - c) \pmod p$
满足二次同余式$x^2 \equiv n \pmod p$
可利用Tonelli–Shanks算法求解secret,然后异或enc便得到了flag:
def Legendre(n,p): #这里用勒让德符号来表示判断二次(非)剩余的过程
return pow(n,(p - 1) // 2,p)
def Tonelli_Shanks(n,p):
assert Legendre(n,p) == 1
if p % 4 == 3:
return pow(n,(p + 1) // 4,p)
q = p - 1
s = 0
while q % 2 == 0:
q = q // 2
s += 1
for z in range(2,p):
if Legendre(z,p) == p - 1:
c = pow(z,q,p)
break
r = pow(n,(q + 1) // 2,p)
t = pow(n,q,p)
m = s
if t % p == 1:
return r
else:
i = 0
while t % p != 1: #外层循环的判断条件
temp = pow(t,2**(i+1),p) #这里写作i+1是为了确保之后内层循环用到i值是与这里的i+1的值是相等的
i += 1
if temp % p == 1: # 内层循环的判断条件
b = pow(c,2**(m - i - 1),p)
r = r * b % p
c = b * b % p
t = t * c % p
m = i
i = 0 # 注意每次内层循环结束后i值要更新为0
return r
num1 = 6023304966622247460261427847144394818572943247946434323275721792843243938440324294324349326166203828252327046668948034768905493329350113405677812338671880
n = inverse(a,p)*(num1 - c)
secret = Tonelli_Shanks(n,p)
import hashlib
flag = enc ^ bytes_to_long(hashlib.sha512(b'%d'%(secret)).digest())
print(long_to_bytes(flag))
#b'Here_is_ur_flag!:)d3ctf{th3_c0oppbpbpbp3rsM1th_i5_s0_1ntr35ting}'
这道题里考的求解二元多项式也很重要。
这两道题只是简单用来下TS算法,其它类型的待补充。
参考:
AntCTF x D^3CTF_Crypto_部分复现_M3ng@L的博客-CSDN博客
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 1666739907@qq.com